An Efficient Alternative to PWM for Embedded Systems
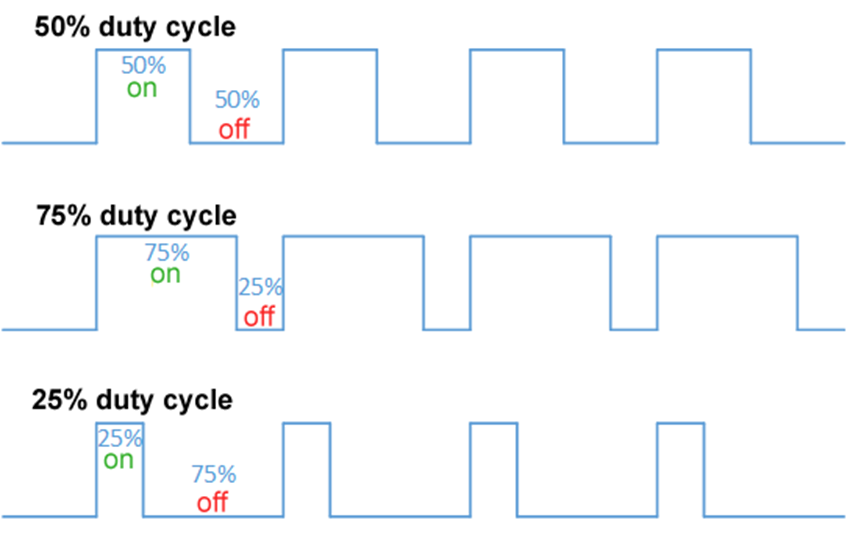
Pulse Width Modulation (PWM) control enjoys broad peripheral support in common microcontrollers and is generally well understood by embedded developers. The microcontroller utilizes a timer to allocate the on time (duty cycle) of a digital output within a defined period. PWM peripherals provide useful functionality for motor control, power supply regulation, and digital to analog conversion.
Proportional Pulse Output (PPO) supports similar applications as PWM using an inverted relationship with the fundamental frequency. While PWM subdivides a single period with an assigned duty cycle, PPO uses fixed divisions of the period to intersperse output pulses across the entire period.
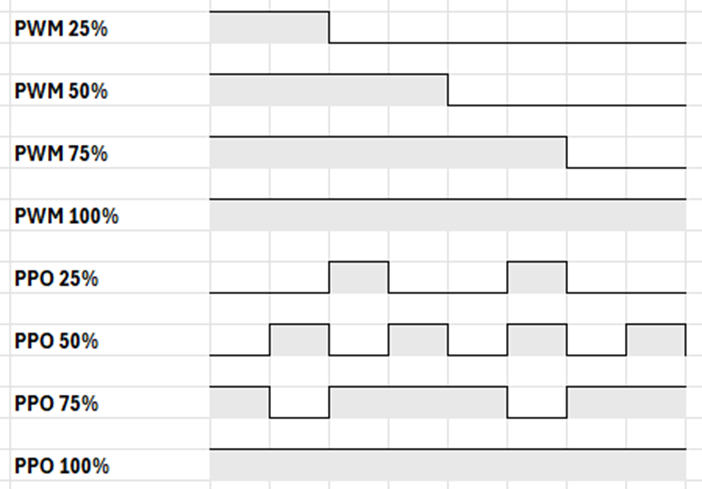
PPO versus PWM
PPO is preferrable to PWM in common high-power AC applications as well as in applications requiring many independent outputs.
Zero-crossing Synchronization
Intermittent energization applications perform switching at zero-crossing to limit electrical interference or comply with control restrictions. Utilizing zero-crossing on 60Hz AC power generates a natural 8.33msec timing division for pulse output.
For example, consider a large-scale AC air heater that requires switching at zero-crossing. PPO allows conduction of power distributed across one second based on 120 half cycles. PID control can be used to control temperature based on setting a simple 0-120 value proportional to the desired power level.
PWM Peripheral Scarcity
Peripheral PWM output channels are a limited resource when implemented using a hardware peripheral. PPO output channels using a consistent time-base only require a single timer and an output pin for each channel.
For example, an application using 4 RGB LEDs would require 12 PWM outputs drive arbitrary color output or specialized LED controllers. PPO would allow the LEDs to be controlled with a single timer and 12 output pins.
Implementation
The primary problem with PPO in embedded applications stems from inefficient or uninformed implementations. PPO coding commonly includes look-up tables or incremental linear calculations using multiplication and division, resulting in excessive memory use (look-up tables) or execution time (calculations) which are not necessary.
What would an efficient PPO algorithm look like? It needs to efficiently determine if the output is on or off in the next iteration. The calculation needs to happen in an interrupt handler with support for multiple channels. To start with, no floating-point math. Better yet, no multiplication or division, even with integers, in the “inner loop.”
Coming up with a solution requires thinking about a problem the right way. The easy way to find the right way is to think like someone who has already solved the problem. Who always has a need for speed – graphics programmers.
What does a proportional output look like in graphics? Easy – that’s a line. Pulses distributed across time instead of rise over run. That seems similar. What’s a fast way to draw a line?
Bresenham’s Line Algorithm
With exposure to computer graphics theory, you’ve may recall Bresenham’s Line Algorithm, or at least have been introduced to incremental error algorithms. When rasterizing, it’s common to use accumulation of an error term to control stepping in discrete space.
Take a side trip to Wikipedia or Michael Abrash’s Graphics Programming Black Book for a detailed explanation.
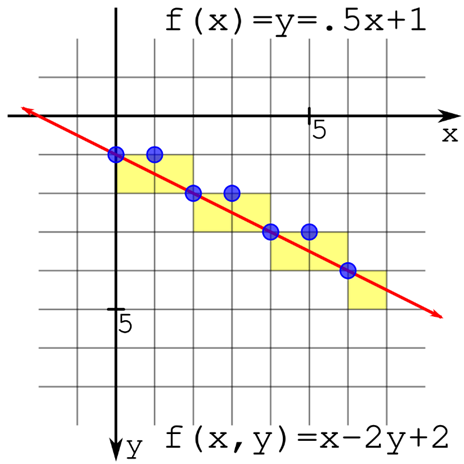
Consider drawing the line y= 0.5x + 1. As we step in the positive x direction, we move only half a pixel in the y direction. But we’re dealing with pixels, not real numbers, and need to determine if a pixel is on or off.
Error is accumulated as we move across the line segment causing bumps in x and y locations. Multiplying the error term by 2 effectively induces rounding at 0.5.
Here’s the pseudocode for the algorithm from the Wikipedia.
plotLine(x0, y0, x1, y1)
dx = abs(x1 - x0)
sx = x0 < x1 ? 1 : -1
dy = -abs(y1 - y0)
sy = y0 < y1 ? 1 : -1
error = dx + dy
while true
plot(x0, y0)
if x0 == x1 && y0 == y1 break
e2 = 2 * error
if e2 >= dy
error = error + dy
x0 = x0 + sx
end if
if e2 <= dx
error = error + dx
y0 = y0 + sy
end if
end whileFrom Lines to Pulses
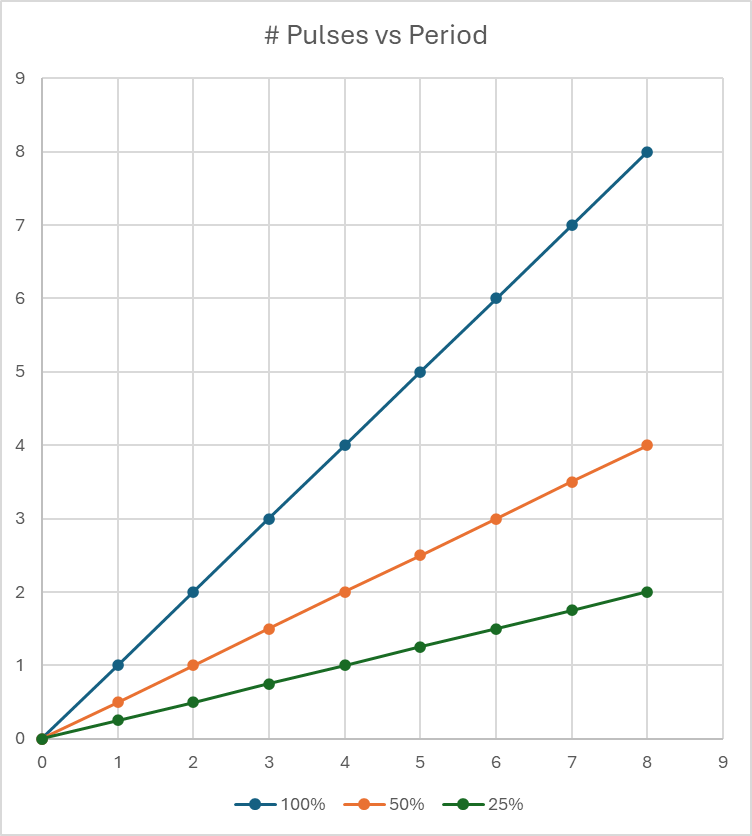
Hopefully, you are starting to see the connection. Instead of working in 2D space, our problem is in the discrete time domain. Instead of X-Y, consider the same algorithm graphed as the number of pulses in the period versus time.
If we are 100% on, pulses would graph as a 45 degree line: y = x, pulses = period. If we are 50% on, pulses would graph as a 22.5 degree line: y = x/2, pulses = period/2.
Convert this to discrete time and let’s rework the plotline pseudocode. Our lines all begin at (0, 0) and run to (span, value), greatly simplifying our calculations.
x0 = 0
y0 = 0
x1 = span
y1 = value
dx = span - 0 = span
dy = value - 0 = value
D = 2*dy - dx = 2*value - span
y = 0
for x from 0 to span
if D > 0
y = y + 1
D = D - 2 * span
end if
D = D + 2 * valueSimplify the results and update some variable names to make it more readable.
error = 2*value - span
output = off
for t from 0 to span
if error > 0
output = on
error = error - 2*span
else
output = off
error = error + 2*valueImplementation in C
Functions to set the status (value and span) and perform the incremental update make up the C implementation.
int error;
bool output;
int value2;
int span2;
void PPO_Set(int value, int span)
{
value2 = value << 1;
span2 = span << 1;
error = value2 - span;
}
bool PPO_Update(void)
{
bool output = false;
if (error > 0)
{
output = true;
error -= span2;
}
error += value2;
return output;
}PPO in Action
A simple demonstration of Proportional Pulse Output generation in action is available on the OnlineGDB online compiler and debugger for C/C++.
Visualizing PPO output is provided by printing out ASCII waveforms of corresponding to value and span. The example to the right shows the output of a run with span 32.
Give it a run to see the waveform output of the values for a 100 span configuration, or fork it to make modifications and experiment with different setups.

PPO in Embedded Systems
Putting the PPO to work in an embedded system requires a handful of changes. An interrupt routine – zero-crossing or periodic time – performs the PPO_Update function. Changing the output uses the PPO_Set function. State (error, span, value) must be maintained for each PPO channel.
While the sample code uses int, signed integers of defined sizes (int8_t, int16_t) work well and can improve performance by matching processor ALU size. Bear in mind that the maximum span supported is half of the maximum signed value (127/2 or 63 for an int8_t).
Conclusions
If you made it through the explanation, at a minimum you’ve added Proportional Pulse Output to your embedded bag of tricks. You’re ready to control a pile of LEDs, bank of fans, or dim a bunch of lights without a matching set of PWM peripherals.
A better result would be gaining insight into how classic algorithms can be repurposed for alternate applications. Rasterization converts graphical data to discrete space. Embedded systems convert signals to discrete time. There are assuredly many more crossover applications.